搜索

标签云

分类

声明

文章若未特別註明，皆採用

請自覺遵守

鏈。。。

存档

匆匆过客

88527

功能

互聯(Federated)社交網絡

2019-04-08: 本文亦在我的新博客中

（本文亦在我的wikiblog中）

互聯社交網絡是除了互聯即時通信系統/IM以外的另一主要互聯系統類型。從來沒有接觸過這類系統的人可以類比互聯的效果爲：直接在新浪微博關注騰訊微博的人（而不需要去騰訊微博重新註冊賬號）。

之前在跟人介紹時，我發現有人會將互聯系統和SSO的效果搞混。事實上，兩者完全不同。仍然以上面在新浪微博S關注騰訊微博T爲例：SSO的本質仍然是在T上註冊了一個新賬戶，然後使用T上的賬戶去關注T上的另一個賬戶，而你的S賬戶上仍然是沒有對T上的關注；但互聯SNS的效果是你直接在S上關注T上的人，不需要在T上重新生成一個賬戶。如果仍然不理解，那請思考在你不登錄T時，即使你做過了“關注”，在你的S賬戶能否看到T上被你關注的人的消息。

幾大比較知名的互聯SNS系統爲：

既然叫互聯系統，每個互聯SNS之內各個不同實例/服務器間的用戶可以互操作。事實上，這些系統主要分爲兩種協議（以及HubZilla的Zot），每個協議內不同系統也可互操作。

下文將以協議爲主要線索串聯不同互聯SNS系統特點與分別、大概歷史、以及我個人對其看法。其中內容來自我對不同互聯SNS系統的瞭解（包括使用），以及背景閱讀（尤其是下文中將會經常引用其圖片的這篇文章）。

The Federation與The Fediverse

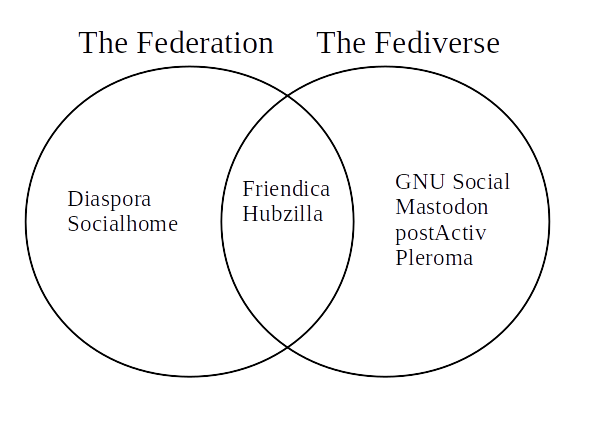（來自https://medium.com/we-distribute/a-quick-guide-to-the-free-network-c069309f334）

一般來說，在OStatus協議（及其衍生協議）下的系統（組成的網絡）被統稱爲The Fediverse；Diaspora協議下的系統（組成的網絡）被稱爲The Federation。

Federation一詞就是“聯邦”之義；Fediverse應該是Federation和Diverse（“多樣的”）兩個詞的組合。

但事實上，如圖中所示，不像商業網絡，The Fediverse和The Federation並非涇渭分明——許多系統同時支持這兩者。比如上面提到但沒有分類的Friendica就同時支持兩個網絡；HubZilla在支持自己的Zot網絡之外，也同時支持這兩者。

之所以最初有協議的分別，除了（不知道有沒有）純粹的感情因素以外，系統的目的是影響協議設計的主要區別。其中，OStatus協議設計爲微博客使用；Diaspora協議被設計來服務更偏Facebook的展板/貼子型社交網絡。於是，The Federation中系統的UI設計脫則胎於Twitter；The Fediverse中系統的UI設計則更偏向Facebook。

OStatus協議這邊稍有更多歷史可講：OStatus協議是GNU Social整合了StatusNet之後爲StatusNet協議改名的產物；而後來，Pump.io在OStatus的基礎上進行了一定改動形成了自己的協議。在2012年冬天之後，OStatus主要被一個W3C工作組維護；而後來，W3C成立了W3C Federated Social Web Working Group，並基於Pump.io的協議制定了新的ActivityPub協議，用以取代OStatus（參考自這裏）。

ActivityPub

2017年W3C將ActivityPub協議立爲推薦的標準，用來取代之前的OStatus協議。

（仍然來自https://medium.com/we-distribute/a-quick-guide-to-the-free-network-c069309f334）

多數網絡均轉向支持ActivityPub協議（且許多系統已經實現ActivityPub），但Diaspora*似乎並沒有做此打算。Nextcloud這一本來並不是SNS的系統也將支持ActivityPub協議，作爲跨站/互聯消息的分發機制。

我個人是比較希望各個網絡可以整合在一個協議之下，以減少維護成本。但ActivityPub畢竟衍生自微博客協議，由於我沒有閱讀過其協議內容，所以對該協議對其他形式內容（比如版面/貼子）的支持存在疑慮。

HubZilla與Zot

HubZilla是一個比較獨特的系統：它沒有選擇使用OStatus或Diaspora協議，而是自己提出了新的Zot協議。就我個人瞭解來看，Zot並不是僅僅另一個協議：Zot最爲標彰的特點是所謂nomadic identity，這一點在其他協議（包括ActivityPub）中並不存在。

簡單來說，nomadic identity允許兩件事：

使用站點A的身份去登錄站點B（同樣，不需要在B上創建賬戶，數據仍然存在A上）
當有需要時，將站點A的身份（包括內容）整個克隆至站點B，並且所有關注了A站點身份的人將自動轉向關注站點B的身份

這兩點特性十分符合我的心意：

遠程認證這點省去了每次遇到新網站均需要重新註冊賬號的麻煩
- 多年來（大約四年），我一直在（時不時）尋找遠程登錄的機制，而找到的最佳機制是OpenID一類。然而，且不說我至今都沒有弄明白的OpenID版本，OpenID在多數網站上仍然被作爲一種SSO實現：之前提過，SSO本質上也是重新註冊。
身份的轉移則是更多考慮站點切換的問題
- 由於允許身份轉移，vender locking的情況會大大降低，迫使服務提供方不能選擇壓榨用戶
- 在特殊情況下（比如站點不再維護），身份的轉移降低了遷移成本

當然，第二條主要在沒有GDPR的時候（+的地區）比較重要——GDPR規定服務商必須允許用戶將自己的數據（用戶自己上傳/填寫的所有數據）導出成機器可讀的格式。但即使是有GDPR，用戶仍然需要想辦法手動告知其他用戶自己的遷移。

在一篇文章中，HubZilla直接被稱爲全包平臺，體現了HubZilla的壯志/野心：HubZilla希望（Zot協議）成爲基礎，並且在其上構建各種服務，包括SNS、論壇、數據存儲……

我個人（四五年來）一直比較希望論壇可以被設計爲互聯系統，但一直沒有找到。HubZilla的設計給了我這個希望，且其實現已經部分涵蓋該目的。

使用體會及總結

我個人最近嘗試過Mastodon、Diaspora*、HubZilla，印象中以前也試過pump.io以及GNU Social但記憶不是很深刻。

首先，必須要強調的是，不同於舊式的中心化社交網絡，互聯社交網絡是去中心化的。去中心化帶來多種便利，但同時也可能會導致從舊時代過來的人思維遇到障礙：互聯社交網絡的“官方”只有項目網站，並沒有“官方實例”（雖然官方一般都提供實例使用，但這僅僅是諸多對等實例中的一個）。想要使用互聯社交網絡，請選擇任意一個你喜歡的實例，或是自己搭建一個實例。一般而言，官方或第三方會維護一份（到多份）實例清單（由於去中心化的本質，清單並不全面，但足夠使用），可以從中選擇一個。

基本而言，Mastodon符合其微博客服務的定位，且功能全面（內容、可見性、API及授權控制）；另外其多欄的UI算是比較有特點，打破多數微博客服務那種中部瀑布的模式。另外，Mastodon似乎沒有爲動態設置地理位置的選項。

Diaspora*符合正常的以主題爲線索的社交網絡（如facebook）定位，但不包含遊戲等功能。當然，完全可以將Diaspora*當作微博客使用。

HubZilla則是一個全功能的平臺，可以當微博客、長文型社交網絡、相冊、論壇……需要注意的是，HubZilla將每一頻道作爲一個主體（每個賬號可以建立多個channel，彼此默認獨立），並且以頻道作爲管理單位。我也試過其nomadic identity，遷移自己的頻道並且保持聯動的更新，其效果的確符合預期。然而HubZilla的界面看起來總有一種奇怪的簡陋感，即使其每個元素並不給人這種感覺。或許自定義主題後會有所改進，但我僅僅嘗試了默認提供的數套主題。

在測試中，每種網絡內互相關注都很輕易；跨網絡的互通測試結果如下（並沒有測試所有可能的組合）：

HubZilla和Mastodon
- HubZilla可以輕易關注Mastodon上的人（以SOME_ONE@MASTODON.INSTANCE形式增加連接）
- Mastodon上可直接搜索HubZilla上的人（只要該HubZilla實例支持和Mastodon互聯，一般爲ActivityPub協議）
- HubZilla上以MASTODON.INSTANCE/SOME_ONE形式關注Mastodon上的人似乎有問題，其頭像右下角會顯示“禁止”圖標
HubZilla關注Daspora*上的人似乎需要對方的審覈（會在其頭像右下角顯示一個“禁止”圖標）

詳細使用體會見部分互聯社交網絡測試感受

如前面所述，整體而言，我更喜歡HubZilla的設計，於是自己在某一HubZilla實例上安了個窩。（具體地址見個人介紹頁面，這裏不再贅述；如果找不到，歡迎用你所知的任何可以聯繫我的方式詢問。）如果是爲非我自己的人推薦，Mastodon應該是我首推的，畢竟無論是功能還是設計上看我個人都很喜歡它。

Rocket使用小結

2019-04-08: 本文亦在我的新博客中

（本文亦在我的wikiblog中）

在今年Increase Rust's Reach中，我參與Rust新網站的i18n及l10n。其中新網站要基於Rocket構建，所以也就（跟着官方教程）學習了一下Rocket。既然學了，就順便記錄一點心得和體會，以方便後來者。

Rocket是一個 web框架。我個人對web編程（尤前端）並不太感興趣（主要是感到 web技術棧太過麻煩/複雜），所以涉及不太多，之前也只用過Python那邊的Flask以及（一小段時間）Django以及Go自帶的http服務器，故而本文不怎麼會涉及和其他web框架的對比。

本文不打算成爲通常意義上的Rocket教程，而只是打算給有興趣者一個快速的（對rocket的）觀感。其中也會有一些個人的經驗教訓等。

Rocket概覽

類似我之前用過的框架，Rocket也將函數作爲不同的路由的處理器。Rocket在每個函數之前使用形如#[get("/myroute")]的屬性作爲標記，之後在Rocket入口對象/結構體上對所需要的路由（函數）進行mount即可。

#[get("/")]
fn index() -> &'static str {
    "Hello, world!"
}

fn main() {
    rocket::ignite()
        .mount("/", routes![index])
        .launch();
}

（代碼片段來自這裏。）

這點粗看很像Flask中使用@app.route()進行路由設定，僅有這兩點不同：

Rocket不使用全局的app對象
路由可以定義但不掛載

我最初也以爲Rocket和Flask的設計極爲相似，且兩者都只打算做web框架而不涉及其他；然而，越到後面越是發現兩者不同之處的巨大。相對而言，我個人更喜歡Rocket的設計：更加函數導向（亦強調使用局部變量）。

在Rocket中，函數是處理路由的全部，不需要使用如flask中魔法一般的全局request對象；
函數的參數和屬性中的設定共同決定了路由是否匹配，手動類型的優勢在這裏有所體現；
各種（預定義或自定義的）請求哨衛可以被添加到函數參數表中參與決定路由的匹配性；
使用整流器在請求到達前或應答發送時對請求或應答進行調整；
使用State做狀態存儲，以便的確需要“全局”變量的情況。

路由匹配

Rocket通過在屬性上設定不同的HTTP方法以及URL段來做匹配。具體細節見官方文檔，這裏僅做摘要：

常見HTTP方法均被支持，只是每次只能設定一個方法
在未定義時，HEAD請求會被自動轉到相應的GET請求上（不過會刪除應答體）
表單首個字段爲_method時，POST請求會被自動重譯爲相應的請求
- 該設定是爲了方便瀏覽器，畢竟瀏覽器通常只有GET和POST

在路由的URL上，可以設定將部分（或全部）節注入到函數的對應參數中。Rocket會自動進行類型轉換，且僅匹配轉換成功的路由。

#[get("/hello/<name>/<age>/<cool>")]
fn hello(name: String, age: u8, cool: bool) -> String {
    if cool {
        format!("You're a cool {} year old, {}!", age, name)
    } else {
        format!("{}, we need to talk about your coolness.", name)
    }
}

（代碼片段來自這裏。）

自定義類型也可用在路由匹配中，只要其實現了FromParam trait即可。

請求及應答

在不考慮整流器的情況下，用戶的請求將直接進入相應的路由函數中，然後經過函數的處理，最後函數的返回值將作爲應答。路由匹配的過程即是請求處理器的選擇過程。

Rocket不要求路由函數的返回值是一個HTTP應答（Response），而是通過Responder機制方便編程：路由函數的返回值需要是一個實現了Responder trait的類型，而Rocket負責調用Responder的相關函數將路由函數的返回值轉換爲HTTP應答。這樣，在Rocket中我們便可以用String等類型作爲函數返回值。

Rocket提供一些實現以應對常見的應答情況：

應答包裝器可以包含其他Responder，並且執行自己的修改
- status可以覆蓋應答中的狀態代碼
- content可以覆蓋應答中的Content-Type字段
- Error（我沒嘗試過，所以直接鏈接至官方文檔）
String和&str會被作爲應答體，且Content-Type會被設置爲text/plain
Option是應答包裝器，Option<T>的T需要實現Responder：
- 當是Some時，其內容將會被作爲應答
- 當是None時，返回404
Result是應答包裝器，且其功能取決於E是否實現Responder：
- 若E實現了Responder，則該Result會被作爲應答（無論是Ok還是Err）
- 若E沒有實現Responder，則Ok會被作爲應答，但Err會被記錄在終端中且返回500

（官方文檔中還列出了幾個常見的對於HTTP很有意義的Responder實現，包括下面所說的Template。）

網頁模板

作爲一個web框架，提供對網頁模板的支持幾乎是理所應當。Rocket本身提供了Template機制，而在rocket_contrib crate中提供了一些特定模板支持。

Template被實現爲一個Responder，這樣讓響應函數返回Template類型即可：

#[get("/")]
fn index() -> Template {
    let context = /* object-like value */;
    Template::render("index", &context)
}

Rocket不限制使用何種模板，但官方文檔提到了.hbs Handlebars和.tera Tera。而Rocket的Template機制之所以有效，還需要整流器的幫助——所以需要在Rocket實例上.attach(Template::fairing());以便可以正確使用模板。

整流器

依Rocket文檔所說，整流器的功能類似於中間件，可以介入請求和應答過程以進行額外操作。由於我沒有學過相關課程，也沒有太多瞭解相關知識，所以無法給出個人對此的看法，只能照搬官方文檔的說法。

在類似其他框架的中間件之外，Rocket對整流器的功能有一些額外規定：

整流器不能終止或直接響應請求
整流器不能任意注入非請求數據至請求中
整流器可以阻止程序的啓動
整流器可以修改程序的配置

官方文檔對整流器有更多說明，但對我來說最需要知道的還有這些：

整流器應當只用於“全局”適用的東西（比如做日誌）
更多時候，需要的其實是請求哨衛和數據哨衛
整流器按順序執行，所以.attach()的順序需要注意

全局共享數據

這裏的“全局”指的是Rocket之內，在各個路由中共享數據。由於路由是由Rocket管理的，故而其參數表中沒辦法添加更多參數；而Rust又沒有全局變量（即使有也不符合美感），故而Rocket提供的狀態機制可謂實用非常。Rocket官方教程中也教導使用狀態來管理數據庫連接。

使用上，狀態同樣通過請求哨衛機制，作爲路由函數的參數。任何類型的數據均可作爲State，且不需要額外實現任何東西。唯一的要求就是在Rocket實例載入時要求管理該狀態。

像這樣要求Rocket去管理某個狀態：

struct HitCount {
    count: AtomicUsize
}

rocket::ignite()
    .manage(HitCount { count: AtomicUsize::new(0) });

像這樣要求在某路由函數上使用某狀態：

#[get("/count")]
fn count(hit_count: State<HitCount>) -> String {
    let current_count = hit_count.count.load(Ordering::Relaxed);
    format!("Number of visits: {}", current_count)
}

#[get("/state")]
fn state(hit_count: State<HitCount>, config: State<Config>) -> T { ... }

需要注意的是，Rocket對每種數據類型管理一個狀態，而不是每個數據。

另外，在自定義的請求哨衛中，也可以使用狀態：

fn from_request(req: &'a Request<'r>) -> request::Outcome<T, ()> {
    let hit_count_state = req.guard::<State<HitCount>>()?;
    let current_count = hit_count_state.count.load(Ordering::Relaxed);
    ...
}

（代碼片段來自這裏。）

總結

總得來說，我個人對Rocket的設計較爲欣賞/膜拜，尤其是其對Rust各項機制的有效利用。

之前用其他框架時總有覺得彆扭的地方，但它們均不存在於Rocket中，讓我寫起來覺得比較順手：

Django（2013年底或2014年初）
- 框架內耦合性太強，但框架的手又過長
- 什麼都想讓框架承包，初學者用起來束手束腳
  - 當然，也可以說是我還沒有體會到Django的好處。但我實在是對封閉花園式的東西感到反感，所以不見得可以體會到Django的妙處
- 而且當年對Py3的支持還不怎麼樣，但我又恰恰想用Py3
Go（2015年）
- Go的自帶http庫直接將請求和應答對象作爲參數傳入，手動解析很難受
- Go的html模板是語言提供的，靈活度上讓我懷疑
- 當時（2015年）查過其他的go語言web框架，比較看好的有beego以及另一個想不起來名稱的。但其教程寫得並不如人意（不如我意），又由於當年需求十分簡單，所以直接裸上語言庫
Flask（2016年）
- Flask要使用全局的app對象和db對象，設計上很詭異
- Flask要使用魔法一般的request對象，總讓人覺得不安心
  - 且request對象暴露太多內容，類似Go用http庫的感覺（和使用Android的Context對象的感覺很像）

然而，我對Rocket的部分trait和/或類型設計仍有疑惑，還在尋找解決方案的過程中。另外，我暫時還沒有在Rust中使用過數據庫連接，所以無法對其聯合使用後的手感做出評價。但綜合來看，Rocket的設計可以說是我所用過的所有框架中最符合我心意的框架；而且它的設計理念可以說符合了我對web框架所構想的所有主要要求。如果不是因爲Rust仍算小衆，Rocket的用戶量和教程量應當早就超過現有的數量了吧（2018-08-02 Google搜“Rust Rocket 教程”，得到11,200條結果）。

Against EU Copyright Directive Article 13

Description

While reading wikipedia these days, there is a new banner calling for against the new "Directive on Copyright in the Digital Single Market" (which will be voted on 5 July) / "EU Copyright directive" / "file 2016/0280(COD)".

The three buttons link to the following pages respectively:

A brief reading shows that many organizations/foundations (e.g. EFF, Creative Commons, Wikimedia Foundation) oppose to this directive.

The context of this directive can be found at: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX:52016PC0593

The main against of this directive is Article 11 and Article 13, especially Article 13.

My words

I should say I agree with many of the disputes that Article 13 should be reformed before applied (explanation at the end). One most probable consequence is that MEMEs will become unavailable. (And this will be one more of the stupid things people have done in recent years, just to satisfy the stale copyright laws.)

I don't know what really works, but I found three sites describing some ways:

Explanation

The texts in the given link differs some bit between what's described in that wikipedia article. I presume this because of the different versions of the document.

Article 13 grants the censoring and blocking ability and obligation to "Information society service providers" (mostly social networking websites, including both commercial ones, e.g. twitter, facebook, and non-commercial ones, e.g. GNUSocial instances, if I understand correctly). This ability suggests them to use "effective content recognition technologies" to "prevent the availability on their services of works or other subject-matter identified by rightholders (through the cooperation with the service providers)".

Although this ability and obligation is supposed to be "appropriate and proportionate", but at least I don't believe commercial bodies (i.e. companies) will do this "appropriately" in a minimal effort way. They will overactive, both for their "compliance with the law" and for their profit purpose. Some companies in China have already demonstrated this, and I guess there are also some examples in Europe and America.

The piece of text says "identified by rightholders", but in reality "rightholders" in many cases are not a single human but a company. We have heard many stories how companies over-use their copyright to prevent what we as humans see as normal behaviours (let alone I don't totally agree with the copyright [law] nowadays because I think they are developed for paper-publishing era not digital era).

The "Information society service providers" are, most of the time, companies; companies are for profit. Therefore, the nature of capital makes them not sympathetic, and blocking the Internet doesn't really affect their profit (because "everyone" does this, leaving us no choice). https://twitter.com/EvenDragsnes/status/1014394747706925056 is definitely not a future I want.

(Terrorism and some other things shall be dealt with, but this directive has nothing to do with that.)

AI在做什麼？我們應該在乎什麼、擔心什麼？

過年自己給自己稍微放鬆幾天，於是有點閒暇時間；加上前兩天聽了兩場報告，分別是《Steps Toward Robust Artificial Intelligence》和《Machine Learning and AI for the Sciences - Towards Understanding》，對AI發展有一點新認識。故而覺得有必要給自己之前的知識做個總結，順便供對AI有興趣但並無太多瞭解的人對現今的AI技術有個概念，並且希望可以讓更多人擔心該擔心的，不在無意義的爭吵浪費時間。

继续阅读